Name | Function | Examples/Description |
@abs(x), abs(x) | absolute value | @abs(-3)=3. |
@bounds(x,y,z) | boundary values | returns 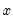 if if 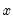 is between is between 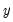 and and 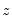 and the boundary values and the boundary values 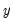 and and 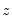 otherwise otherwise |
@ceiling(x[,n]) | smallest integer not less than | @ceiling(2.34)=3, @ceiling(4)=4. |
@exp(x), exp(x) | exponential, 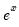 | @exp(1)=2.71813. |
@expm1(x) | exponential, 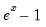 | For x near zero. |
@fact(x) | factorial, 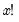 | @fact(3)=6, @fact(0)=1. |
@factlog(x) | natural logarithm of the factorial, 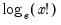 | @factlog(3)=1.79176, @factlog(0)=0. |
@floor(x[,n]) | largest integer not greater than | @floor(1.23)=1, @floor(-3.1)=-4. |
@iff(s,x,y) | recode by condition | returns 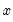 if condition if condition 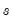 is true; otherwise returns is true; otherwise returns 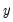 . Note this is the same as @recode. . Note this is the same as @recode. |
@inv(x) | reciprocal, 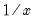 | inv(2)=0.5 (For series only; you should use
@einv to obtain the element inverse of a matrix). |
@mod(x,y) | floating point remainder | returns the remainder of 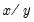 with the same sign as with the same sign as 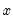 . If . If 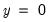 the result is 0. the result is 0. |
@log(x), log(x) | natural logarithm, 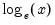 | @log(2)=0.693..., log(@exp(1))=1. |
@log1p(x) | 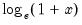 | For 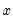 near zero. near zero. |
@log1mexp(x) | 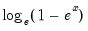 | For negative 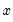 near zero. near zero. |
@log10(x) | base-10 logarithm, 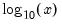 | @log10(100)=2. |
@logx(x,b) | base-b logarithm, 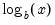 | @logx(256,2)=8. |
@nan(x,y) | recode NAs in X to Y | returns 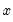 if if 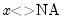 , and , and 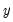 if if 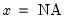 . . |
@pmax(x,y) | pairwise max | returns the pairwise max of 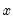 and and 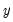 (for more than pairs, use @rmax) (for more than pairs, use @rmax) |
@pmin(x,y) | pairwise min | returns the pairwise max of 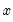 and and 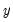 (for more than pairs, use @rmin) (for more than pairs, use @rmin) |
@pow(x,a) | power, 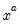 | @pow(2,3) = 8. |
@powm1(x,a) | 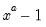 | For 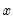 near one. near one. |
@pow1pm1(x,a) | 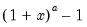 | For 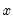 near zero. While similar to @powm1, this function supports a full double-precision “delta” from one. Among other things, this allows exponentiation of values extremely close to one that cannot be represented in double-precision, e.g., near zero. While similar to @powm1, this function supports a full double-precision “delta” from one. Among other things, this allows exponentiation of values extremely close to one that cannot be represented in double-precision, e.g., 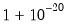 . This function should only be used if the calculation of . This function should only be used if the calculation of 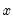 naturally falls near zero. If the calculation of naturally falls near zero. If the calculation of 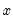 naturally falls near one, @powm1 should be used instead. Supplying naturally falls near one, @powm1 should be used instead. Supplying 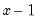 to this function will produce less accurate results. to this function will produce less accurate results. |
@recode(s,x,y) | recode by condition | returns 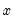 if condition if condition 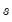 is true; otherwise returns is true; otherwise returns 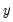 . . |
@round(x[,n]) | round to the nearest integer | @round(-97.5)=-98, @round(3.5)=4. |
@sign(x) | returns sign of 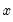 | returns -1, 0, 1 depending on the sign of the corresponding element of 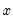 |
@sqrt(x), sqr(x) | square root | @sqrt(9)=3. |