Function | Description |
@beta(a,b) | beta integral (Euler integral of the second kind): 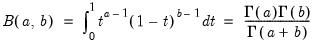 for 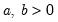 . . |
@betainc(x,a,b[,n]) | incomplete beta integral: 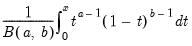 for 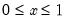 and and 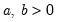 . . |
@betaincder(x,a,b,s) | derivative of the incomplete beta integral: evaluates the derivatives of the incomplete beta integral  , where , where 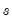 is an integer from 1 to 9 corresponding to the desired derivative: is an integer from 1 to 9 corresponding to the desired derivative: 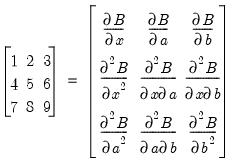 |
@betaincinv(p,a,b) | inverse of the incomplete beta integral: returns an 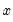 satisfying: satisfying: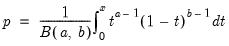 for 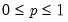 and and  . . |
@betalog(a,b) | natural logarithm of the beta integral: 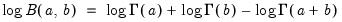 . . |
@binom(n,x) | binomial coefficient: 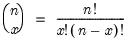 for 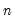 and and 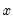 positive integers, positive integers, 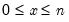 . . |
@binomlog(n,x) | natural logarithm of the binomial coefficient:  |
@cloglog(x) | complementary log-log function: 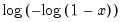 See also @qextreme. |
@digamma(x), @psi(x) | first derivative of the log gamma function: 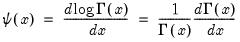 |
@erf(x) | error function: 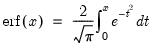 for 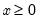 . . |
@erfc(x) | complementary error function: 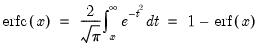 . .for 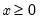 . . |
@gamma(x) | (complete) gamma function: 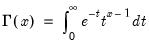 for 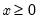 . . |
@gammader(x) | first derivative of the gamma function: 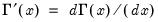 Note: Euler’s constant,  , may be evaluated as , may be evaluated as 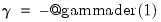 . See also @digamma and @trigamma. . See also @digamma and @trigamma. |
@gammainc(x,a[,n]) | incomplete gamma function: 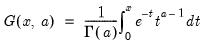 for  and and 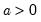 . . |
@gammaincder(x,a,n) | derivative of the incomplete gamma function: Evaluates the derivatives of the incomplete gamma integral 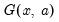 , where , where 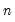 is an integer from 1 to 5 corresponding to the desired derivative: is an integer from 1 to 5 corresponding to the desired derivative: 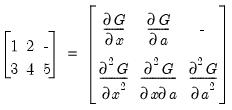 |
@gammaincinv(p,a) | inverse of the incomplete gamma function: find the value of 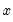 satisfying: satisfying: for 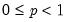 and and 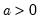 . . |
@gammalog(x) | logarithm of the gamma function: 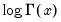 . For derivatives of this function see @digamma and @trigamma. . For derivatives of this function see @digamma and @trigamma. |
@logit(x) | logistic transform: 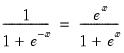 |
@psi(x) | see @digamma. |
@trigamma(x) | second derivative of the log gamma function: 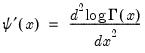 |