QR decomposition of matrix.
Syntax: @qr(M, R[, P])
M: matrix
R: matrix
P: (optional) matrix
Return: matrix
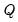
Decomposes an

matrix
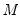
into an

orthogonal matrix
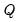
and an
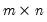
upper triangular matrix
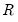
such that
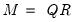
, where
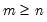
.
If permutation matrix
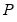
is provided, the decomposition produces
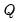
and
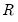
such that
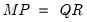
.
Examples
matrix m1 = @mnrnd(7, 5)
matrix r
matrix q = @qr(m1, r)
generates a random matrix M1, then decomposes it into the orthogonal matrix Q, and the upper triangular matrix R.
The following illustrate the properties of the decomposition:
sym i1 = @inner(q)
matrix m2 = q * r
where I1 is the identity matrix, and M2 is equal to M1.
Cross-references
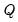
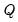
 matrix
matrix 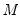 into an
into an  orthogonal matrix
orthogonal matrix 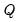 and an
and an 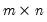 upper triangular matrix
upper triangular matrix 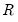 such that
such that 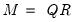 , where
, where 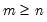 .
. 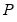 is provided, the decomposition produces
is provided, the decomposition produces 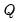 and
and 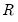 such that
such that 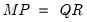 .
.