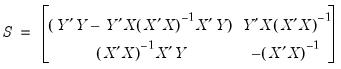Sweep operator.
There are two syntaxes for @sweep, one for the symmetric, and the other for then non-symmetric operator.
Syntax: @sweep(s[, n])
s: sym
k: integer
k2: (optional) integer
Return: matrix
Returns the result of applying the symmetric sweep operator to symmetric matrix S at diagonal element k. If k2 is specified, sweeps on all diagonal elements between k and k2, inclusive.
Syntax: @sweep(m, r, c)
m: matrix, sym
r: integer
c: integer
Return: matrix
Returns the result of applying the non-symmetric sweep operator to general matrix m at element (r, c).
The sweep operator is an elementary matrix row operation with particularly useful properties when applied to uncorrected sum of squares and cross-products (USSCP) matrices. Among these properties is the ability to calculate the coefficients for one or more regressions over a common set of regressors.
Let
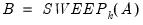
be an application of the symmetric sweep operator. Then,
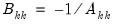
,
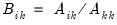
where
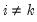
,
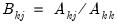
where
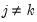
, and
where
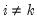
and
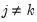
.
Let
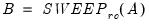
be an application of the non-symmetric sweep operator. Then,
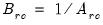
,
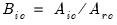
where
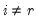
,
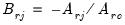
where
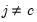
, and
where
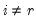
and
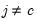
.
Examples
As an example of using the sweep operator to replicate the results of OLS regression, suppose we have series for one dependent variable, Y, and three regressors, X1, X2, X3
We can organize the data into a group YX = [Y X1 X2 X3], form the USSCP matrix (YX)'YX, and apply the sweep operator to the three diagonal elements associated with the regressors (elements 2-4).
Each application of the sweep operator to a diagonal element effectively switched the role of the associated variable from dependent to regressor.
workfile u 1000
series y = nrnd
series x1 = nrnd
series x2 = nrnd
series x3 = nrnd
group g y x1 x2 x3
sym usscp = @inner(g)
sym S = @sweep(usscp, 2, 4)
The resulting block matrix will have the form:
This matrix contains all the information usually associated with the results of OLS regression, which we can extract.
vector beta = @subextract(S, 2, 1, 4, 1) ' Regressor coefficients
scalar SSR = S(1,1) ' Sum of squared residuals
sym invXtX = -@subextract(S, 2, 2)
vector se = @sqrt(SSR * @getmaindiagonal(invXtX) / (@obssmpl - 3)) ' Coefficient standard errors
We could compare these results to those of a standard equation object for the same regression.
equation eq.ls(noconst) y x1 x2 x3
It is also possible to conduct multiple regressions against a set of common regressors. Consider a small example with two dependent variables, y1 and y2, and two regressors, x1 and x2. We proceed as before, again applying the sweep operator to only the two diagonal elements associated with regressors (3-4).
series y1 = nrnd
series y2 = nrnd
group g1 y1 y2 x1 x2
sym usscp1 = @inner(g1)
sym S1 = @sweep(usscp, 3, 4)
matrix beta1 = @subextract(S1, 3, 1, 4, 2)
vector SSR1 = @getmaindiagonal(@subextract(S1, 1, 1, 2, 2))
sym invXtX1 = -@subextract(S1, 3, 3)
vector se1 = @sqrt(@kronecker(SSR1, @getmaindiagonal(invXtX1)) / (@obssmpl - 2))
Again, we could compare these results to those of standard equation objects.
equation eq1.ls(noconst) y1 x1 x2
equation eq2.ls(noconst) y2 x1 x2
Cross-references
Goodnight, James H. (1979). “A Tutorial on the SWEEP Operator,” The American Statistician, 33, 149–158.
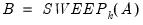 be an application of the symmetric sweep operator. Then,
be an application of the symmetric sweep operator. Then, 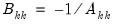 ,
, 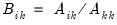 where
where 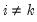 ,
, 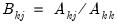 where
where 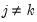 , and
, and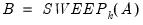 be an application of the symmetric sweep operator. Then,
be an application of the symmetric sweep operator. Then, 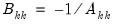 ,
, 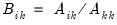 where
where 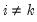 ,
, 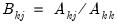 where
where 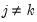 , and
, and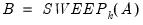 be an application of the symmetric sweep operator. Then,
be an application of the symmetric sweep operator. Then, 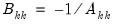 ,
, 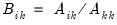 where
where 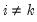 ,
, 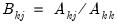 where
where 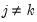 , and
, and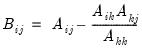
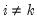 and
and 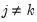 .
.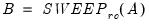 be an application of the non-symmetric sweep operator. Then,
be an application of the non-symmetric sweep operator. Then, 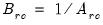 ,
, 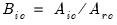 where
where 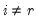 ,
, 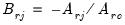 where
where 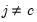 , and
, and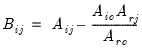
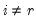 and
and 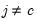 .
.