Background
The explosion in available data over recent decades, coupled with increases in computing power, has led to the growing popularity of methods that allow the data themselves to suggest the most appropriate combination of regressors to use in estimation. These techniques allow the researcher to provide a set of candidate variables for the model, rather than specifying a specific model.
Variable selection techniques are implemented in EViews as a pre-estimation step before performing a standard least squares regression. Before estimation, you must specify a dependent variable together with a list of always-included variable, and a list of selection variables, from which the selection algorithm will choose the most appropriate. Following the variable selection process, EViews reports the results of the final regression, i.e. the regression of the always-included and the selected variables on the dependent variable.
In some cases the sample used in this equation may not coincide with the regression that was used during the selection process. This will occur if some of the omitted search variables have missing values for some observations that do not have missing values in the final regression. In such cases EViews will print a warning in the regression output.
The p-values listed in the final regression output and all subsequent testing procedures do not account for the regressions that were run during the selection process. One should take care to interpret results accordingly.
Variable Selection Methods
EViews offers five different variable selection methods: Uni-directional, Stepwise, Swapwise, Combinatorial, Auto-Search/GETS and Lasso Selection.
Uni-Directional
Uni-Directional-Forwards
The Uni-directional-Forwards method uses either a lowest p-value or largest t-statistic criterion for adding variables.
The method begins with no added regressors. If using the p-value criterion, we select the variable that would have the lowest p-value were it added to the regression. If the p-value is lower than the specified stopping criteria, the variable is added. The selection continues by selecting the variable with the next lowest p-value, given the inclusion of the first variable. The procedure stops when the lowest p-value of the variables not yet included is greater than the specified forwards stopping criterion, or the number of forward steps or number of added regressors reach the optional user specified limits.
If using the largest t-statistic criterion, the same variables are selected, but the stopping criterion is specified in terms of the statistic value instead of the p-value.
Uni-Directional-Backwards
The Uni-directional-Backwards method is analogous to the Uni-directional-Forwards method, but begins with all possible added variables included, and then removes the variable with the highest p-value. The procedure continues by removing the variable with the next highest p-value, given that the first variable has already been removed. This process continues until the highest p-value is less than the specified backwards stopping criteria, or the number of backward steps or number of added regressors reach the optional user specified limits.
The largest t-statistic may be used in place of the lowest p-value as a selection criterion.
Stepwise
Stepwise-Forwards
The Stepwise-Forwards method is a combination of the Uni-directional-Forwards and Backwards methods. Stepwise-Forwards begins with no additional regressors in the regression, then adds the variable with the lowest p-value. The variable with the next lowest p-value given that the first variable has already been chosen, is then added. Next both of the added variables are checked against the backwards p-value criterion. Any variable whose p-value is higher than the criterion is removed.
Once the removal step has been performed, the next variable is added. At this, and each successive addition to the model, all the previously added variables are checked against the backwards criterion and possibly removed. The Stepwise-Forwards routine ends when the lowest p-value of the variables not yet included is greater than the specified forwards stopping criteria (or the number of forwards and backwards steps or the number of added regressors has reached the corresponding optional user specified limit).
You may elect to use the largest t-statistic may be used in place of the lowest p-value as a selection criterion.
Stepwise-Backwards
The Stepwise-Backwards procedure reverses the Stepwise-Forwards method. All possible added variables are first included in the model. The variable with the highest p-value is first removed. The variable with the next highest p-value, given the removal of the first variable, is also removed. Next both of the removed variables are checked against the forwards p-value criterion. Any variable whose p-value is lower than the criterion is added back in to the model.
Once the addition step has been performed, the next variable is removed. This process continues where at each successive removal from the model, all the previously removed variables are checked against the forwards criterion and potentially re-added. The Stepwise-Backwards routine ends when the largest p-value of the variables inside the model is less than the specified backwards stopping criterion, or the number of forwards and backwards steps or number of regressors reaches the corresponding optional user specified limit.
The largest t-statistic may be used in place of the lowest p-value as a selection criterion.
Swapwise
The swapwise methods both begin with no additional regressors in the model.
Swapwise-Max R-Squared Increment
The Max R-squared Increment method starts by adding the variable which maximizes the resulting regression R-squared. The variable that leads to the largest increase in R-squared is then added. Next each of the two variables that have been added as regressors are compared individually with all variables not included in the model, calculating whether the R-squared could be improved by swapping the “inside” with an “outside” variable. If such an improvement exists then the “inside” variable is replaced by the “outside” variable. If there exists more than one swap that would improve the R-squared, the swap that yields the largest increase is made.
Once a swap has been made the comparison process starts again. Once all comparisons and possible swaps are made, a third variable is added, with the variable chosen to produce the largest increase in R-squared. The three variables inside the model are then compared with all the variables outside the model and any R-squared increasing swaps are made. This process continues until the number of variables added to the model reaches the user-specified limit.
Swapwise-Min R-Squared Increment
The Min R-squared Increment method is very similar to the Max R-squared method. The difference lies in the swapping procedure. Whereas the Max R-squared swaps the variables that would lead to the largest increase in R-squared, the Min R-squared method makes a swap based on the smallest increase. This can lead to a more lengthy selection process, with a larger number of combinations of variables compared.
Combinatorial
For a given number of added variables, the combinatorial method evaluates every possible combination of added variables, and selects the combination that leads to the largest R-squared in a regression using the added and always included variables as regressors. This method is more thorough than the previous methods, since those methods do not compare every possible combination of variables, and obviously requires additional computation. With large numbers of potential added variables, the Combinatorial approach can take a very long time to complete.
Auto-Search / GETS
The auto-search/GETS algorithm follows the steps suggested by AutoSEARCH algorithm of Escribano and Sucarrat (2011), which in turn builds upon the work in Hoover and Perez 1999. The algorithm is similar to the uni-directional-backwards method:
1. The model with all search variables (termed the general unrestricted model, GUM) is estimated, and checked with a set of diagnostic tests.
2. A number of search paths are defined, one for each insignificant search variable in the GUM.
3. For each path, the insignificant variable defined in 2) is removed and then a series of further variable removal steps is taken, each time removing the most insignificant variable, and each time checking whether the current model passes the set of diagnostic tests. If the diagnostic tests fail after the removal of a variable, that variable is placed back into the model and prevented from being removed again along this path. Variable removal finishes once there are no more insignificant variables, or it is impossible to removal a variable without failing the diagnostic tests.
4. Once all paths have been calculated the final models produced by the paths are compared using an information criteria selection. The best model is then selected.
For the suite of diagnostic tests performed on both the GUM and in each path, EViews includes:
• AR LM test—a Q-statistic test on the level residuals at the specified significance and number of lags.
• ARCH LM test—a Q-statistic test on the squared residuals at the specified significance and number of lags.
• A Jarque-Bera normality test.
• A parsimonious encompassing test (PET)—for models other than the GUM, an F-test of the overall significance of the removed regressors compared to the GUM.
• Auto-search/GETS allows for cases where there are more search variables than observations in the estimation sample – a situation typically impossible due to singularity of the regressor matrix. In such cases the algorithm is split into blocks, where each block has its own GUM with a subset of the search regressors. The algorithm works through each block individually, and then combines the individually selected variables from each block into a new GUM and runs one more time.
Lasso
The
Lasso (Least-Absolute Shrinkage and Selection Operator) estimator is a regression estimator with an
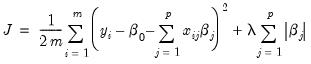
penalty term that is acts to guard against over-fitting. The
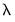
term penalizes non-zero coefficients, pushing (shrinking) them toward zero. This behavior is termed
shrinkage.
The Lasso objective function is
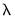 | (22.1) |
with the overall penalty parameter
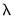
and the individual penalty weights
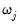
acting to determine the extent of the penalty and to control the degree of shrinkage.
The Lasso variable selection method implemented in EViews is a model selection routine that estimates models for one or more penalty parameters
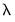
, possibly performing cross-validation to determine an optimal
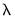
, and uses the results to determine the set of admissible regressors. Variables whose coefficients shrink to zero in the optimal Lasso specification are excluded from the selected model.
While Lasso is a powerful tool for model selection, caution should be used when applying Lasso to models with highly collinear variables, as this method tends to select one variable at random from a group of such variables.
See “
“Elastic Net and Lasso” for additional discussion.
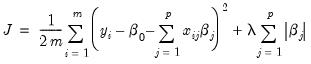 penalty term that is acts to guard against over-fitting. The
penalty term that is acts to guard against over-fitting. The 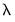 term penalizes non-zero coefficients, pushing (shrinking) them toward zero. This behavior is termed shrinkage.
term penalizes non-zero coefficients, pushing (shrinking) them toward zero. This behavior is termed shrinkage.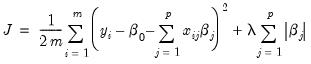 penalty term that is acts to guard against over-fitting. The
penalty term that is acts to guard against over-fitting. The 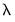 term penalizes non-zero coefficients, pushing (shrinking) them toward zero. This behavior is termed shrinkage.
term penalizes non-zero coefficients, pushing (shrinking) them toward zero. This behavior is termed shrinkage.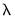
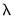 and the individual penalty weights
and the individual penalty weights 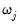 acting to determine the extent of the penalty and to control the degree of shrinkage.
acting to determine the extent of the penalty and to control the degree of shrinkage. 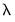 , possibly performing cross-validation to determine an optimal
, possibly performing cross-validation to determine an optimal 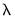 , and uses the results to determine the set of admissible regressors. Variables whose coefficients shrink to zero in the optimal Lasso specification are excluded from the selected model.
, and uses the results to determine the set of admissible regressors. Variables whose coefficients shrink to zero in the optimal Lasso specification are excluded from the selected model.