For each observation 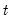 corresponding to a row in the group of
corresponding to a row in the group of 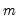 series, compute the q-quantile of the
series, compute the q-quantile of the 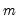 values
values 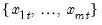 for the observation using the Rankit-Cleveland quantile definition, for
for the observation using the Rankit-Cleveland quantile definition, for 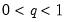 .
.
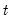 corresponding to a row in the group of
corresponding to a row in the group of 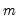 series, compute the q-quantile of the
series, compute the q-quantile of the 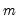 values
values 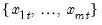 for the observation using the Rankit-Cleveland quantile definition, for
for the observation using the Rankit-Cleveland quantile definition, for 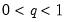 .
.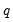 -quantile, first find
-quantile, first find 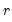 , the smallest rank such that,
, the smallest rank such that,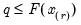
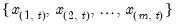 represent data for the
represent data for the 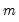 series ordered from low to high, and
series ordered from low to high, and 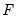 is the Rankit-Cleveland definition of the empirical distribution function:
is the Rankit-Cleveland definition of the empirical distribution function: 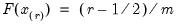 . For purposes of computing
. For purposes of computing 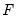 , tied ranks are assumed to take the last tied value.
, tied ranks are assumed to take the last tied value.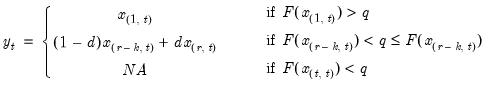

 the smallest integer where
the smallest integer where 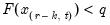 . In the leading case where there are no tied
. In the leading case where there are no tied 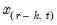 values,
values, 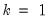 .
.