Working with a GLM Equation
EViews offers various views and procedures for a estimated GLM equation. Some, like the or the coefficient view are self-explanatory. In this section, we offer relevant comment on the remaining views.
Residuals
The main equation output offers summary statistics for the sum-of-squared response residuals (“Sum squared resid”), and the sum-of-squared Pearson residuals (“Pearson SSR”).
The views and allow you to examine properties of your residuals. The and , show the fit of the unweighted data. As the name suggests, the displays the standardized (scaled Pearson) residuals.
The show of the standardized residuals and of the standardized residuals and the squared standardized residuals.
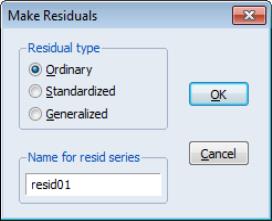
The proc allows you to save the (response), (scaled Pearson), or (score) residuals into the workfile. The latter may be useful for constructing test statistics (note, however, that in some cases, it may be more useful to compute the gradients of the model directly using ).
Given standardized residuals SRES for equation EQ1, the unscaled Pearson residuals may be obtained using the command
series pearson = sres * @sqrt(eq1.@dispersion)
Forecasting
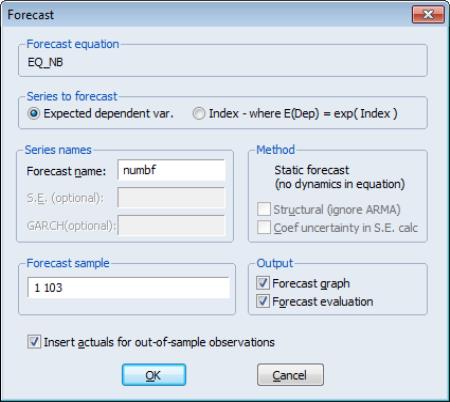
EViews offers built-in tools for producing in and out-of-sample forecasts (fits) from your GLM estimated equation. Simply click on the button on your estimated equation to bring up the forecast dialog, then enter the desired settings.
You should first use the radio buttons to specify whether you wish to forecast the expected dependent variable
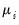
or the linear index
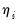
.
Next, enter the name of the series to hold the forecast output, and set the forecast sample.
Lastly, specify whether you wish to produce a forecast graph and whether you wish to fill non-forecast values in the workfile with actual values or to fill them with NAs. For most cross-section applications, we recommend that you uncheck this box.
Click on to produce the forecast.
Note that while EViews does not presently offer a menu item for saving the fitted GLM variances or scaled variances, you can easily obtain results by saving the ordinary and standardized residuals and taking ratios (
“Residuals”). If ORESID are the ordinary and SRESID are the standardized residuals for equation EQ1, then the commands
series glmsvar = (oresid / sresid)^2
series glmvar = glmvar * eq1.@dispersion
produce the scaled variance and unscaled variances, respectively.
Lastly, you should use to create a model object for more complicated simulation from your GLM equation.
Testing
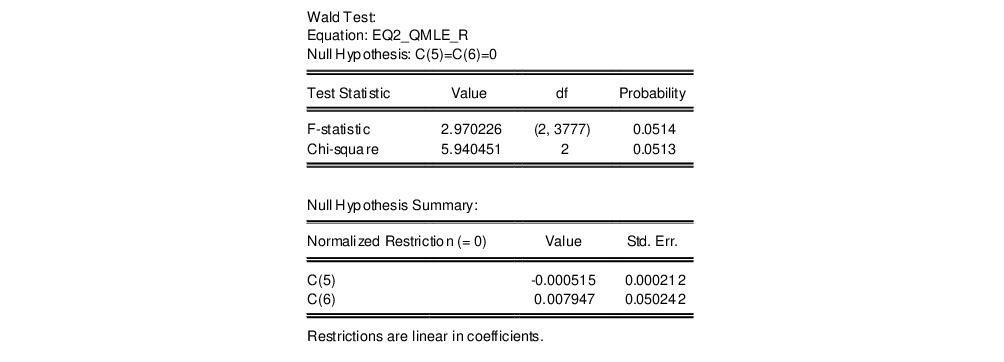
You may perform Wald tests of coefficient restrictions. Simply select , then enter your restrictions in the edit field. For the Papke-Wooldridge example above with Huber-White robust covariances, we may use a Wald test to evaluate the joint significance of AGE^2 and SOLE by entering the restriction “C(5)=C(6)=0” and clicking on OK to perform the test.
The test results show joint-significance at just above the 5% level. The and views will also employ the robust covariance matrix estimates.
The and views and the views are likelihood ratio based tests. Note that the RESET test is a special case of an omitted variables test where the omitted variables are powers of the fitted values from the original equation.
We illustrate these tests by performing the RESET test on the first Papke-Wooldridge QMLE equation with GLM covariances. Select and change the default to include 2 fitted terms in the test equation.
The top portion of the output shows the test settings, and the test summaries. The bottom portion of the output shows the estimated test equation. The results show little evidence of nonlinearity.
Notice that in contrast to LR tests in most other equation views, the likelihood ratio test statistics in GLM equations are obtained from analysis of the deviances or quasi-deviances. Suppose
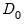
is the unscaled deviance under the null and
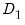
is the corresponding statistic under the alternative hypothesis. The usual asymptotic
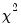
likelihood ratio test statistic may be written in terms of the difference of deviances with common scaling,
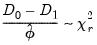 | (32.4) |
as
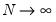
, where
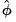
is an estimate of the dispersion and
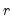
is the fixed number of restrictions imposed by the null hypothesis.

is either a specified fixed value or an estimate under the alternative hypothesis using the specified dispersion method. When
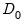
and
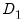
contain the quasi-deviances, the resulting statistic is the quasi-likelihood ratio (QLR) statistic (Wooldridge, 1997).
If
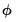
is estimated, we may also employ the
F-statistic variant of the test statistic:
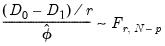 | (32.5) |
where
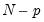
is the degrees-of-freedom under the alternative and
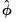
is an estimate of the dispersion. EViews will estimate
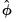
under the alternative hypothesis using the method specified in your equation.
We point out that the Ramsey test results (and all other GLM LR test statistics) presented here may be problematic since they rely on the GLM variance assumption, Papke and Wooldridge offer a robust LM formulation for the Ramsey RESET test. This test is not currently built-into EViews, but which may be constructed with some effort using auxiliary results provided by EViews (see Papke and Wooldridge, p. 625 for details on the test construction).

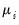 or the linear index
or the linear index 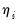 .
.

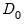 is the unscaled deviance under the null and
is the unscaled deviance under the null and 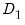 is the corresponding statistic under the alternative hypothesis. The usual asymptotic
is the corresponding statistic under the alternative hypothesis. The usual asymptotic 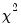 likelihood ratio test statistic may be written in terms of the difference of deviances with common scaling,
likelihood ratio test statistic may be written in terms of the difference of deviances with common scaling, 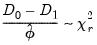
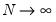 , where
, where 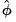 is an estimate of the dispersion and
is an estimate of the dispersion and 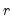 is the fixed number of restrictions imposed by the null hypothesis.
is the fixed number of restrictions imposed by the null hypothesis.  is either a specified fixed value or an estimate under the alternative hypothesis using the specified dispersion method. When
is either a specified fixed value or an estimate under the alternative hypothesis using the specified dispersion method. When 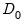 and
and 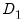 contain the quasi-deviances, the resulting statistic is the quasi-likelihood ratio (QLR) statistic (Wooldridge, 1997).
contain the quasi-deviances, the resulting statistic is the quasi-likelihood ratio (QLR) statistic (Wooldridge, 1997).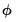 is estimated, we may also employ the F-statistic variant of the test statistic:
is estimated, we may also employ the F-statistic variant of the test statistic: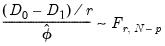
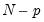 is the degrees-of-freedom under the alternative and
is the degrees-of-freedom under the alternative and 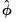 is an estimate of the dispersion. EViews will estimate
is an estimate of the dispersion. EViews will estimate 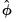 under the alternative hypothesis using the method specified in your equation.
under the alternative hypothesis using the method specified in your equation.