| | |
Beta | @cbeta(x,a,b[,n]), @dbeta(x,a,b), @qbeta(p,a,b), @rbeta(a,b) | for 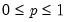 and for 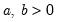 , where 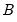 is the @beta function. |
Binomial | @cbinom(x,n,p), @dbinom(x,n,p), @qbinom(s,n,p), @rbinom(n,p) | if 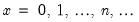 , and 0 otherwise, for 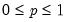 . |
Chi-square | @cchisq(x,v[,n]), @dchisq(x,v), @qchisq(p,v), @rchisq(v) | where 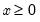 , and 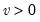 . Note that the degrees of freedom parameter 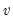 need not be an integer. In addition, the @chisq(x,v) function may be used to obtain the p-values directly. |
Exponential | @cexp(x,m[,n]), @dexp(x,m), @qexp(p,m), @rexp(m) | for 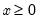 , and 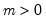 . |
Extreme Value (Type I-minimum) | @cextreme(x[,n]), @dextreme(x), @qextreme(p), @cloglog(p), @rextreme | for 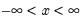 . |
F-distribution | @cfdist(x,v1,v2[,n]), @dfdist(x,v1,v2), @qfdist(p,v1,v2), @rfdist(v1,v1) | where 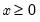 , and 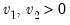 . Note that the functions allow for fractional degrees of freedom parameters 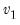 and 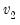 . |
Gamma | @cgamma(x,b,r[,n]), @dgamma(x,b,r), @qgamma(p,b,r), @rgamma(b,r) | where 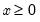 , and 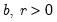 . |
Generalized Error | @cged(x,r[,n]), @dged(x,r), @qged(p,r), @rged(r) | where 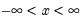 , and 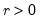 . |
Laplace | @claplace(x[,n]), @dlaplace(x), @qlaplace(x), @rlaplace | for 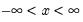 . |
Logistic | @clogistic(x[,n]), @dlogistic(x), @qlogistic(p), @rlogistic | for 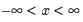 . |
Log-normal | @clognorm(x,m,s[,n]), @dlognorm(x,m,s), @qlognorm(p,m,s), @rlognorm(m,s) | |
Negative Binomial | @cnegbin(x,n,p), @dnegbin(x,n,p), @qnegbin(s,n,p), @rnegbin(n,p) | if 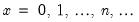 , and 0 otherwise, for 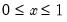 . |
Normal (Gaussian) | @cnorm(x[,n]), @dnorm(x), @qnorm(p), @rnorm, nrnd, @logcnorm | for 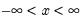 . @logcnorm is a more numerically stable function for the computation of @log(@cnorm(x)) |
Poisson | @cpoisson(x,m), @dpoisson(x,m), @qpoisson(p,m), @rpoisson(m) | if 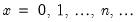 , and 0 otherwise, for 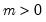 . |
Pareto | @cpareto(x,k,a[,n]), @dpareto(x,k,a), @qpareto(p,k,a), @rpareto(k,a) | for location parameter 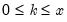 and shape parameter 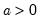 . |
Student's 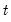 ‑distribution | @ctdist(x,v[,n]), @dtdist(x,v), @qtdist(p,v), @rtdist(v) | for 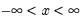 , and 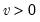 . Note that 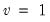 , yields the Cauchy distribution. |
Uniform | @cunif(x,a,b), @dunif(x,a,b), @qunif(p,a,b), @runif(a,b), rnd | for 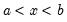 and 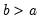 . |
Weibull | @cweib(x,m,a[,n]), @dweib(x,m,a), @qweib(p,m,a), @rweib(m,a) | where 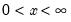 , and 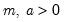 . |
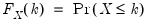 . The quantile functions will return the smallest value where the CDF evaluated at the value equals or exceeds the probability of interest:
. The quantile functions will return the smallest value where the CDF evaluated at the value equals or exceeds the probability of interest: 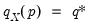 , where
, where 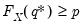 . The inequalities are only relevant for discrete distributions.
. The inequalities are only relevant for discrete distributions.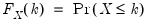 . The quantile functions will return the smallest value where the CDF evaluated at the value equals or exceeds the probability of interest:
. The quantile functions will return the smallest value where the CDF evaluated at the value equals or exceeds the probability of interest: 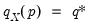 , where
, where 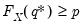 . The inequalities are only relevant for discrete distributions.
. The inequalities are only relevant for discrete distributions.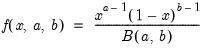
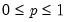 and for
and for 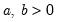 , where
, where 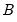 is the
is the 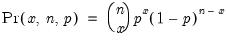
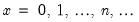 , and 0 otherwise, for
, and 0 otherwise, for 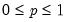 .
.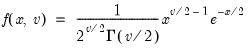
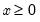 , and
, and 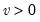 . Note that the degrees of freedom parameter
. Note that the degrees of freedom parameter 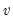 need not be an integer.
need not be an integer. 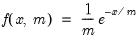
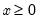 , and
, and 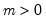 .
.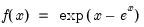
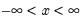 .
.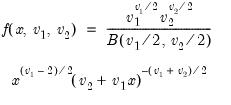
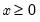 , and
, and 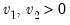 . Note that the functions allow for fractional degrees of freedom parameters
. Note that the functions allow for fractional degrees of freedom parameters 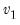 and
and 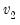 .
.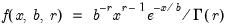
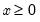 , and
, and 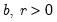 .
.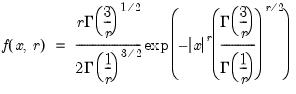
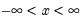 , and
, and 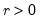 .
.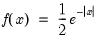
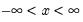 .
.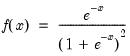
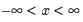 .
.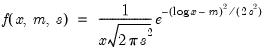
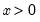 ,
, 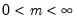 , and
, and 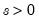 .
.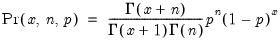
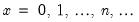 , and 0 otherwise, for
, and 0 otherwise, for 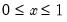 .
.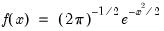
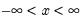 .
. 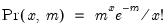
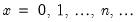 , and 0 otherwise, for
, and 0 otherwise, for 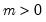 .
.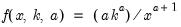
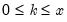 and shape parameter
and shape parameter 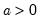 .
.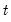 ‑distribution
‑distribution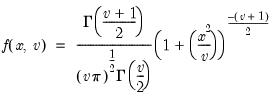
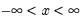 , and
, and 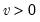 . Note that
. Note that 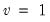 , yields the Cauchy distribution.
, yields the Cauchy distribution.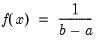
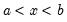 and
and 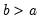 .
.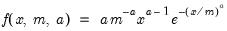
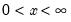 , and
, and 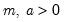 .
.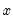 and
and 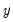 for a distribution with means 0, variances 1, and correlation
for a distribution with means 0, variances 1, and correlation 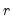 .
.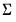 . This form is more efficient when performing multiple draws from the same distribution (compute the Cholesky once, but sample many times).
. This form is more efficient when performing multiple draws from the same distribution (compute the Cholesky once, but sample many times).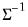 . This form is more efficient than explicitly inverting
. This form is more efficient than explicitly inverting 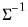 to supply
to supply 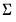 .
.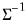 . This form combines the efficiencies of the above forms.
. This form combines the efficiencies of the above forms.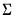 with
with 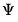
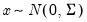 , where
, where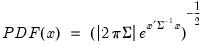
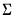 is positive semi-definite.
is positive semi-definite.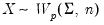 , where
, where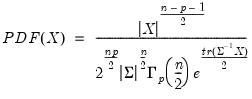 ,
,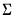 are
are 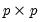 positive definite matrices, and the degrees-of-freedom parameter
positive definite matrices, and the degrees-of-freedom parameter 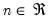 and
and 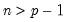 .
.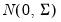 , i.e.,
, i.e., 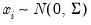 ,
,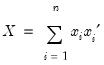 ,
,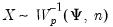 , where
, where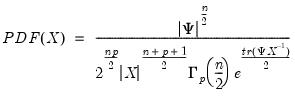 ,
,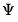 are
are 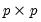 positive definite matrices, and the degrees-of-freedom parameter
positive definite matrices, and the degrees-of-freedom parameter 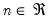 and
and 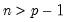 .
.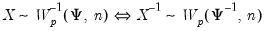 , so there are many relations among the Wishart and inverse Wishart functions, e.g.,
, so there are many relations among the Wishart and inverse Wishart functions, e.g., 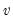 degrees of freedom exceeds
degrees of freedom exceeds 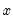 :
: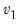 numerator degrees of freedom and
numerator degrees of freedom and 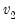 denominator degrees of freedom exceeds
denominator degrees of freedom exceeds 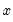 :
: 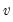 degrees of freedom exceeds
degrees of freedom exceeds 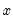 in absolute value (two-sided
in absolute value (two-sided