Empirical quantile.
Compute the quantile value where approximately 100*q percent of the data is less than or equal to the value,
Syntax: @quantile(x, q[, m, s])
x: series, vector, matrix
q: number, series, vector, matrix
m: (optional) string
s: (optional) sample string or object when x is a series and assigning to a series
Return: number
• The quantile value
q must satisfy
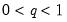
.
• m is an optional string controlling the method of calculating the empirical distribution function: “b” (Blom), “r” (Rankit-Cleveland), “o” (Ordinary), “t” (Tukey), “v” (van der Waerden), “g” (Gumbel). The default value is “r”.
Rankit-Cleveland (default) | |
Ordinary | |
Van der Waerden | |
Blom | |
Tukey | |
Gumbel | |
To compute the

-quantile, first find
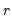
, the smallest rank such that,
where the order statistics
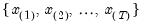
represent data for the
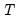
observations ordered from low to high, and
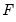
is the assumed empirical distribution function. For purposes of computing

, tied ranks are assumed to take the last tied value.
Then the quantile is computed as
where the interpolating constant is
for
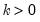
the smallest integer where
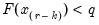
. In the leading case where there are no tied
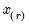
values,
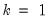
.
For series calculations, EViews will use the current or specified workfile sample.
Examples
= @quantile(x, 0.5)
returns the median of the series x.
= @quantile(x, 0.1)
returns the first decile (10th percentile) of the series x.
Cross-references
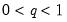 .
.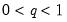 .
.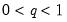 .
.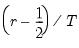
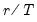



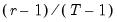
 -quantile, first find
-quantile, first find 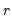 , the smallest rank such that,
, the smallest rank such that,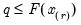
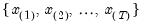 represent data for the
represent data for the 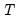 observations ordered from low to high, and
observations ordered from low to high, and 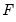 is the assumed empirical distribution function. For purposes of computing
is the assumed empirical distribution function. For purposes of computing  , tied ranks are assumed to take the last tied value.
, tied ranks are assumed to take the last tied value.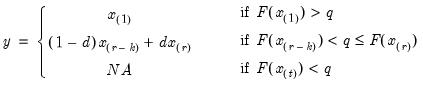
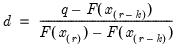
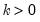 the smallest integer where
the smallest integer where 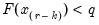 . In the leading case where there are no tied
. In the leading case where there are no tied 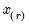 values,
values, 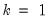 .
.