EViews 10 New Econometrics and Statistics: Estimation

Smooth Threshold Regression (STR and STAR)

EViews 9 introduced Threshold Regression (TR) and Threshold Autoregression (TAR) models, and EViews 10 expands up these model by adding Smooth Threshold Regression and Smooth Threshold Autoregression as options.

In STR models the regime switching that occurs when an observed variable crosses unknown thresholds happens smoothly. As a result, STR models are often considered to have more “realistic” dynamics that their discrete TR model counterparts.

EViews' implementation of STR includes features such as:

• Estimation of parameters for both shape and location of the smooth threshold.
• Model selection for the threshold variable.
• Specification of both regieme varying and regieme non-varying regressors.

Robust Standard Error Additions

EViews has included both White and Heteroskedasticity and Autocorrelation Consistent Covariance (HAC) estimators of the least-squares covariance matrix for over twenty years.

EViews 10 expands upon these robust standard error options with the addition of a family of heteroskedastic consistent covariance, and clustered standard errors.

Heteroskedastic Consistent (HC) Covariance Estimators

EViews 10 increases the options for heteroskedastic consistent covariance estimators beyond the familiar White estimator available in previous versions. The class of estimators supported belong to the HC family described by Long and Ervin, 2000, and Cribari-Neto and da Silva, 2011.

The estimators differ in their choice of observation-specific weights used to improve the finite sample properties of the residual error covariance.

Specifically, EViews supports the following estimators and weight choices:

$$ \begin{array}{|l|c|} \hline \hfill \text{Method} \hfill & \text{Weight}\\ \hline \text{HC0 - White} & 1\\ \hline \text{HC1 - White with d.f. correction} & \sqrt{T/(T-k)}\\ \hline \text{HC2 - bias corrected} & (1-h_t)^{-1/2}\\ \hline \text{HC3 - pseudo-jacknife} & (1-h_t)^{-1}\\ \hline \text{HC4 - relative leverage} & (1-h_t)^{-\delta_t/2}\\ \hline \text{HC4m} & (1-h_t)^{-\gamma_t/2}\\ \hline \text{HC5} & (1-h_t)^{-\delta_t/4}\\ \hline \text{User - user specified} & \text{arbitrary} \\ \hline \end{array} $$ where $h_t = X_t^\top \left(X^\top X\right)^{-1}X_t$ are the diagonal elements of the familiar "hat matrix" $H = X^\top \left(X^\top X\right)^{-1}X$, and $\delta_t$ and $\gamma_t$ are discount factors.

Cluster-Robust Covariance Estimators

In many settings, observations may be grouped into different groups or “clusters” where errors are correlated for observations in the same cluster and uncorrelated for observations in different clusters. EViews 10 offers support for consistent estimation of coefficient covariances that are robust to either one and two-way clustering.

As with the HC estimators, EViews supports a class of cluster-robust covariance estimators, with each estimator differing on the weights it gives to observations in the cluster.

The weighting of each estimator is as follows:

$$ \begin{array}{|l|c|} \hline \hfill \text{Method} \hfill & \text{Weight}\\ \hline \text{CR0 - Ordinary} & 1\\ \hline \text{CR1 - finite sample corrected (default)} & \sqrt{\frac{G}{(G-1)} \cdot \frac{(T-1)}{(T-k)}}\\ \hline \text{CR2 - bias corrected} & (1-h_t)^{-1/2}\\ \hline \text{CR3 - pseudo-jacknife} & (1-h_t)^{-1}\\ \hline \text{CR4 - relative leverage} & (1-h_t)^{-\delta_t/2}\\ \hline \text{CR4m} & (1-h_t)^{-\gamma_t/2}\\ \hline \text{CR5} & (1-h_t)^{-\delta_t/4}\\ \hline \text{User - user specified} & \text{arbitrary} \\ \hline \end{array} $$ where $h_t = X_t^\top \left(X^\top X\right)^{-1}X_t$ are the diagonal elements of the familiar "hat matrix" $H = X^\top \left(X^\top X\right)^{-1}X$, $\delta_t$ and $\gamma_t$ are discount factors, and $G$ is the number of clusters.

VARs with Linear Restrictions

The basic $k$-variable VAR(p) specification has $k(pk+d)$ coefficients so that even moderate sized VARs require estimation of a large number of parameters. When VARs are applied to macroeconomic data with limited sample sizes, model over-parameterization is a frequent problem as there are too few observations to estimate precisely the VAR parameters.

EViews now offers support for the linear restriction approach to handling this over-parameterization problem.

Structural VAR Restrictions

One of the key elements behind Structural VAR estimation is the necessary imposition of restrictions on the residual structure matrices.

These restrictions generally take the form of restrictions on the factorization matrices, A and B, restrictions on the short-run impulse response matrix S, or restrictions on the long-run impulse response matrix F (or C), or a combination of the above.

Previous versions of EViews only allowed restrictions on A and B, or on F. EViews 10 broadens the restriction engine by allowing restrictions on any of the four matrices, adding linear restrictions, and adds a new interface allowing easier specification of the restrictions.

VAR Historical Decomposition

In EViews 10 you may now, from an estimated standard VAR, easily perform historical decomposition, the innovation-accounting technique proposed by Burbridge and Harrison (1985).

Historical decomposition decomposes forecast errors into components associated with structural innovations (computed by weighting ordinary residuals).

Improved nonlinear forecasting

Dynamic forecasting using simulation methods is now supported from the equation forecast dialog.

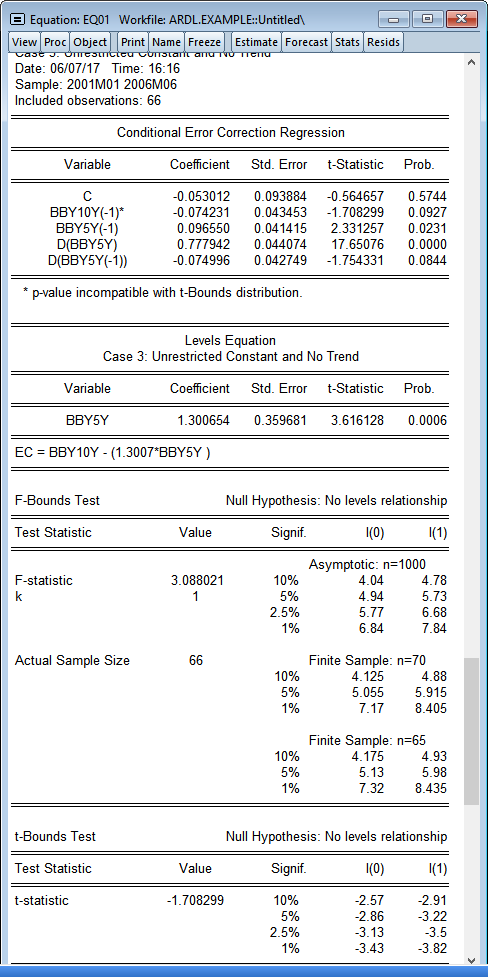
Additional Autoregressive Distributed Lag (ARDL) Tools

Autoregressive Distributed Lag (ARDL) estimation has been drastically improved for EViews 10. In particular, EViews now allows absolute control over lag specification.

Any of the variables (dependent or regressor) can be specified with a custom lag, and you can mix the specification allowing certain variable to have fixed custom lags and the remainder having their lags chosen via model selection methods.

Moreover, in the context of the ARDL approach to the Bounds Cointegration Test of Pesaran Shin and Smith (2001) (PSS), EViews now offers inference under all 5 deterministic cases considered in PSS. Also, alongside the asymptotic critical values provided in PSS, EViews now offers finite sample critical values from Narayan (2005)

Finally, in addition to the Bounds F-test, Eviews now also reports the appropriate Banerjee, Dolado, Mestre (1998) (BDM) t-bounds test.